Project
Investigation of droplet motion in turbulent flows by a VoF-DNS method
For the simulation of turbulent dispersed liquid-liquid flows at large scales, Computational Fluid Dynamics
(CFD) coupled with Population Balance Modelling (PBM) is widely employed [1]. Since droplet interfaces are
not resolved in the CFD-PBM approach, coalescence and breakup of droplets is approximated with sub-grid scale closures. For these closures, the time-averaged root mean square (RMS) droplet fluctuation velocity 𝑈rms,d is a decisive input quantity. The model by Kuboi et al. [2] is most frequently applied for the prediction of 𝑈 rms,d, but it is limited to droplet sizes that fall in the inertial sub-range of turbulent length scales. To overcome this limitation, Solsvik & Jakobsen [3] proposed a model for the prediction of 𝑈rms,d considering the entire spectrum of turbulent length scales. To the best of our knowledge, a verification of the model from [3] by Direct Numerical Simulations (DNS) has not been presented up to now. Therefore, DNS together with an interface-resolving Volume-of-Fluid (VoF) method were employed in the latest project period to study the motion of single droplets in a generic Forced Homogeneous Isotropic Turbulent (FHIT) flow. A parameter study was conducted to investigate the effect of the initial droplet diameter 𝐷 on 𝑈rms,d, and the DNS results were used to assess themodel equation proposed in [3].
Project Details
Project term
May 1, 2023–June 2, 2024
Affiliations
Ruhr University Bochum
Institute
Chair of Hydraulic Fluid Machinery
Principal Investigator
Methods
Simulations were performed with the finite-volume based CFD code OpenFOAM version ESI-v2112. A
segregated pressure-based time-implicit flow solver was used. The Pressure-Implicit with Splitting of Operators
(PISO) [4] algorithm was employed for pressure-velocity coupling. In this algorithm, non-linear outer loops of
the predictor-corrector method are omitted for faster convergence. This was justified since the Courant-
Friedrich-Lewy number 𝐶𝐹𝐿 was kept below 0.05 according to Pope’s criterion for DNS [5], which corresponded
to a time step of Δ𝑡 = 2 ∙ 10−6 [s]. Performing additional non-linear outer loops was also tested, but the effect
on the statistical flow quantities was negligible. A second-order Crank-Nicolson scheme was used for time
discretization, and spatial discretization was performed with second-order central difference schemes. The flow
domain was a cube of edge length 𝐿 = 2𝜋 [mm] with periodic boundaries on each face as depicted in Figure 1.
The computational grid consisted of 3003 = 27 Mio. cubical cells with a constant cell width Δ𝑥 in each direction.
All simulations were conducted at a Taylor-scale Reynolds number of 𝑅𝑒𝜆≈58. According to Pope [5], an accurate spatial resolution of the smallest turbulent length scales is ensured if the ratio between Δ𝑥 and the Kolmogorov length 𝜂 remains below 2.1. This criterion was verified by on-the-fly monitoring [6]. For the simulation of FHIT flows, the momentum equation was complemented with a linear forcing term [7]. A single-phase precursor DNS was carried out for 50 eddy turn-over times, which was long enough for the statistical convergence of the flow field. The latest instantaneous flow field was used for the initialization of the droplet-laden two-phase FHIT simulations. For the resolution of the droplet interface, the geometric VoF method by Scheufler & Roenby [8] was compared with the native algebraic VoF method available in OpenFOAM [9]. VoF methods are prone to the generation of spurious currents, which manifest as purely numerical vortical flow structures in the vicinity of the phase interface [8,9]. Hence, preliminary investigations on a static droplet test case were conducted. It was observed that the characteristic velocity of the spurious currents was orders of magnitude smaller when the geometric VoF method was used compared to the algebraic VoF method. Therefore, the geometric VoF method was applied for the two-phase FHIT simulations. Both the density and viscosity ratio between the continuous and droplet phase were kept at unity. For each droplet, the Weber number based on the RMS fluctuation velocity in the continuous phase 𝑈rms,con was kept constant at a small value of 0.5 to prevent droplet breakup. The initial droplet diameter 𝐷 was varied between approximately 10𝜂 and 50𝜂, so that droplet sizes cover the entire spectrum of turbulent length scales. All two-phase flow simulations were carried out for 30 eddy turn-over times, which was long enough for the statistical convergence of 𝑈rms,d. Additional two-phase FHIT simulations were conducted to ensure the quality of the numerical method. For the test case with 𝐷≈50𝜂, the numerical time step was reduced to Δ𝑡=1∙10−6 [s] and Δ𝑡=0.5∙10−6 [s], which did not show any significant influence on 𝑈rms,d. Hence, the originally chosen value Δ𝑡=2∙10−6 [s] was deemed sufficiently small.
Results
In Figure 2a, the turbulent energy spectrum 𝐸 of our single-phase DNS results is compared with the model spectrum by Pope [5] and the DNS results by Komrakova [10], who investigated a very similar FHIT test case in terms of the computational grid and 𝑅𝑒𝜆. Our single-phase DNS results are in good agreement with both reference curves. Thus, our numerical method employed for DNS of FHIT flows is considered as validated. In Figure 2b, the two-phase DNS results are shown in terms of the RMS droplet fluctuation velocity 𝑈rms,d together with the model equation by Solsvik & Jakobsen [3]. To indicate the statistical uncertainty of the DNS results for 𝑈rms,d, the corresponding standard error of the mean is represented as a vertical bar bounded by two horizontal caps. For the smallest droplet, 𝑈rms,d is very close to the RMS fluctuation velocity in the continuous phase 𝑈rms,con according to our DNS results. This result is consistent with turbulence theory, since droplets of a size below the Kolmogorov length follow their surrounding turbulent flow field like tracer particles [11,12]. For an increasing droplet diameter, 𝑈rms,d decreases monotonically. We attribute this observation to the isotropic character of the turbulence. In HIT flows, velocity vectors decorrelate over larger length scales [5]. Hence, the distribution of velocity vectors in the vicinity of the droplet interface becomes broader when the droplet becomes larger. In turn, the directional preference of fluid motion becomes less pronounced in the vicinity of the droplet interface, leading to a smaller value of 𝑈rms,d. However, an opposite trend is predicted for 𝑈rms,d by the model Figure 1: Instantaneous snapshot of the dimensionless velocity magnitude on the mid-planes of a two-phase FHIT flow together with the interface of a droplet with an initial diameter of 𝐷≈50𝜂. from [3]. A large disparity between our DNS results and the model from [3] becomes discernible for almost all droplet sizes. Thus, improving the model equation from [3] is deemed necessary at least for the flow conditions investigated during this project period. After a further investigation on the effect of the viscosity ratio has beenconducted, a publication of our results in a journal article is planned.
Additional Project Information
DFG classification: 404-03 Fluid Mechanics
Software: OpenFOAM
Cluster: CLAIX
Publications
Gyubbenet, A. (2024). Evaluating Direct Numerical Simulations of Forced Homogeneous Isotropic Turbulent
Flow Using Statistical Methods. Project thesis, Ruhr University Bochum.
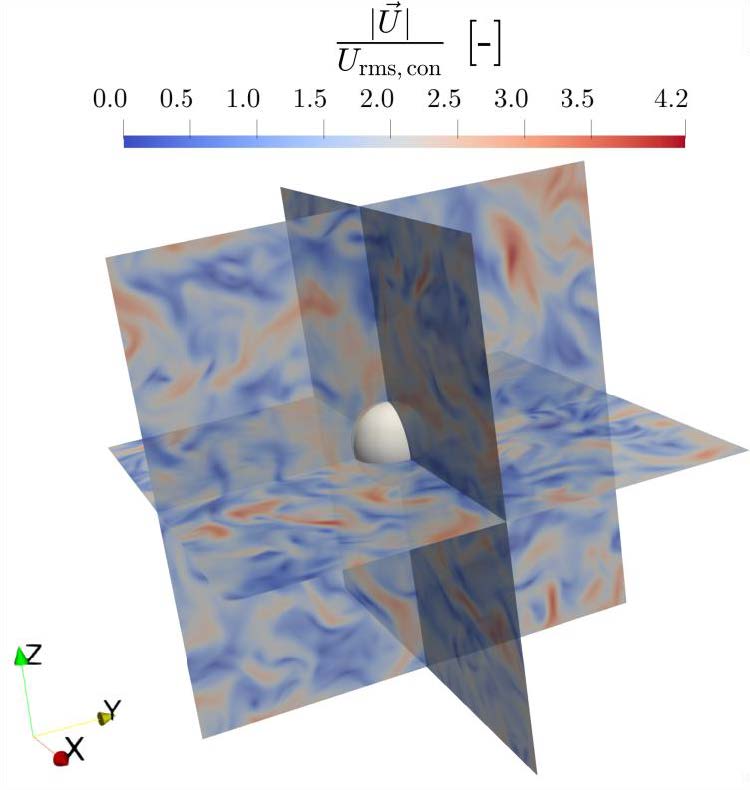 Figure 1: Instantaneous snapshot of the dimensionless velocity magnitude on the mid-planes of a two-phase FHIT flow together with the interface of a droplet with an initial diameter of 𝐷≈50𝜂.
Figure 1: Instantaneous snapshot of the dimensionless velocity magnitude on the mid-planes of a two-phase FHIT flow together with the interface of a droplet with an initial diameter of 𝐷≈50𝜂. 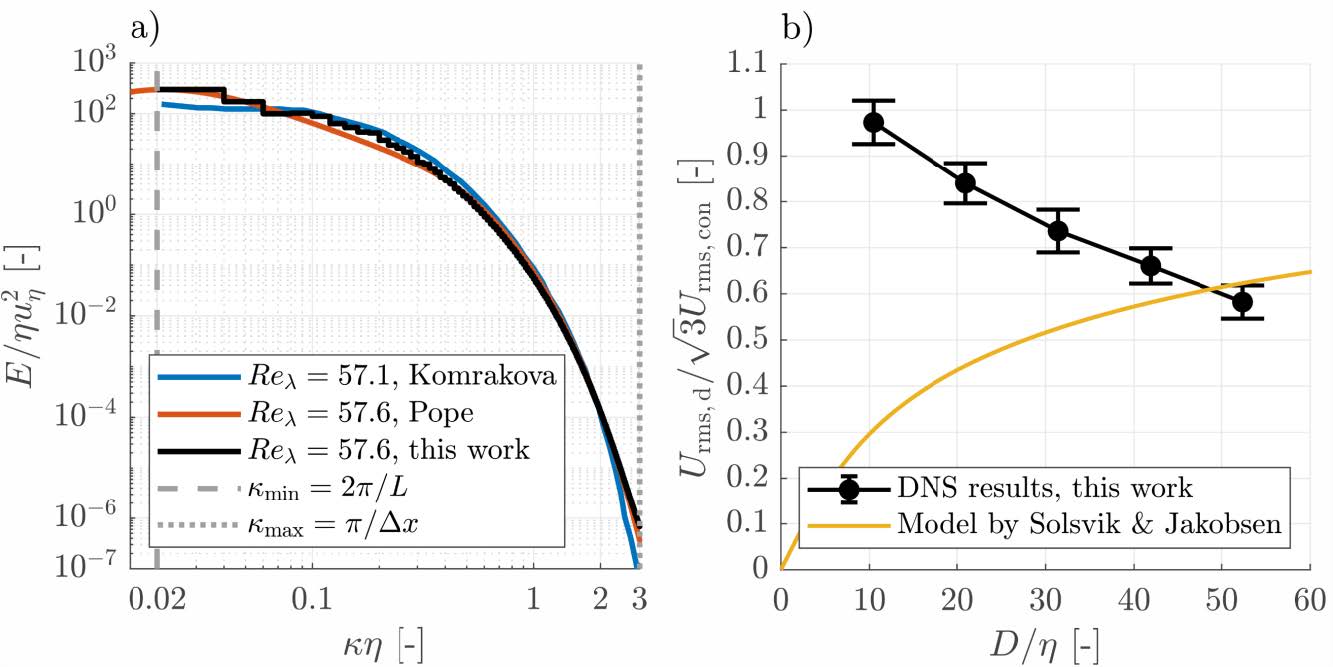 Figure 2: a) Dimensionless turbulent energy spectrum 𝐸𝜂⁄𝑢𝜂2 against the dimensionless wavenumber 𝜅𝜂 of the single-phase precursor DNS in comparison with Pope’s model spectrum [5] and DNS results by Komrakova [10]. b) Dimensionless RMS droplet fluctuation velocity 𝑈𝑟𝑚𝑠,𝑑√3⁄𝑈
Figure 2: a) Dimensionless turbulent energy spectrum 𝐸𝜂⁄𝑢𝜂2 against the dimensionless wavenumber 𝜅𝜂 of the single-phase precursor DNS in comparison with Pope’s model spectrum [5] and DNS results by Komrakova [10]. b) Dimensionless RMS droplet fluctuation velocity 𝑈𝑟𝑚𝑠,𝑑√3⁄𝑈